Example for a latent class analysis with the poLCA-package in R
When you work with R for some time, you really start to wonder why so many R packages have some kind of pun in their name. Intended or not, the poLCA package is one of them. Today i´ll give a glimpse on this package, which doesn´t have to do anything with dancing or nice dotted dresses.
This article is kind of a draft and will be revised anytime.
The „poLCA“-package has its name from „Polytomous Latent Class Analysis“. Latent class analysis is an awesome and still underused (at least in social sciences) statistical method to identify unobserved groups of cases in your data. Polytomous latent class analysis is applicable with categorical data. The unobserved (latent) variable could be different attitude-sets of people which lead to certain response patterns in a survey. In marketing or market research latent class analysis could be used to identify unobserved target-groups with different attitude structures on the basis of their buy-decisions. The data would be binary (not bought, bought) and depending on the products you could perhaps identify a class which chooses the cheapest, the most durable, the most environment friendly, the most status relevant […] product. The latent classes are assumed to be nominal. The poLCA package is not capable of sampling weights, yet.
By the way: There is also another package for latent class models called „lcmm“ and another one named „mclust„.
What does a latent class analysis try to do?
A latent class model uses the different response patterns in the data to find similar groups. It tries to assign groups that are „conditional independent“. That means, that inside of a group the correlations between the variables become zero, because the group membership explains any relationship between the variables.
Latent class analysis is different from latent profile analysis, as the latter uses continous data and the former can be used with categorical data.
Another important aspect of latent class analysis is, that your elements (persons, observations) are not assigned absolutely, but on probability. So you get a probability value for each person to be assigned to group 1, group 2, […], group k.
Before you estimate your LCA model you have to choose how many groups you want to have. You aim for a small number of classes, so that the model is still adequate for the data, but also parsimonious.
If you have a theoretically justified number of groups (k) you expect in your data, you perhaps only model this one solution. A typical assumption would be a group that is pro, one group contra and one group neutral to an object. Another, more exploratory, approach would be to compare multiple models – perhaps one with 2 groups, one with 3 groups, one with 4 groups – and compare these models against each other. If you choose this second way, you can decide to take the model that has the most plausible interpretation. Additionally you could compare the different solutions by BIC or AIC information criteria. BIC is preferred over AIC in latent class models, but usually both are used. A smaller BIC is better than a bigger BIC. Next to AIC and BIC you also get a Chi-Square goodness of fit.
I once asked Drew Linzer, the developer of PoLCA, if there would be some kind of LMR-Test (like in MPLUS) implemented anytime. He said, that he wouldn´t rely on statistical criteria to decide which model is the best, but he would look which model has the most meaningful interpretation and has a better answer to the research question.
Latent class models belong to the family of (finite) mixture models. The parameters are estimated by the EM-Algorithm. It´s called EM, because it has two steps: An „E“stimation step and a „M“aximization step. In the first one, class-membership probabilities are estimated (the first time with some starting values) and in the second step those estimates are altered to maximize the likelihood-function. Both steps are iterative and repeated until the algorithm finds the global maximum. This is the solution with the highest possible likelihood. That´s why starting values in latent class analysis are important. I´m a social scientist who applies statistics, not a statistician, but as far as i understand this, depending on the starting values the algorithm can stop at point where one (!) local maximum is reached, but it might not be the „best“ local maximum (the global maximum) and so the algorithm perhaps should´ve run further. If you run the estimation multiple times with different starting values and it always comes to the same solution, you can be pretty sure that you found the global maximum.
data preparation
Latent class models don´t assume the variables to be continous, but (unordered) categorical. The variables are not allowed to contain zeros, negative values or decimals as you can read in the poLCA vignette. If your variables are binary 0/1 you should add 1 to every value, so they become 1/2. If you have NA-values, you have to recode them to a new category. Rating Items with values from 1-5 should could be added a value 6 from the NAs.
mydata[is.na(mydata)] <- 6
Running LCA models
First you should install the package and define a formula for the model to be estimated.
install.packages("poLCA")
library("poLCA")
# By the way, for all examples in this article, you´ll need some more packages:
library("reshape2")
library("plyr")
library("dplyr")
library("poLCA")
library("ggplot2")
library("ggparallel")
library("igraph")
library("tidyr")
library("knitr")
# these are the defaults of the poLCA command
poLCA(formula, data, nclass=2, maxiter=1000, graphs=FALSE, tol=1e-10, na.rm=TRUE, probs.start=NULL, nrep=1, verbose=TRUE, calc.se=TRUE)
#estimate the model with k-classes
k<-3
lc<-poLCA(f, data, nclass=k, nrep=30, na.rm=FALSE, Graph=TRUE)
The following code stems from this article. It runs a sequence of models with two to ten groups. With nrep=10 it runs every model 10 times and keeps the model with the lowest BIC.
# select variables
mydata <- data %>% dplyr::select(F29_a,F29_b,F29_c,F27_a,F27_b,F27_e,F09_a, F09_b, F09_c)
# define function
f<-with(mydata, cbind(F29_a,F29_b,F29_c,F27_a,F27_b,F27_e,F09_a, F09_b, F09_c)~1) #
#------ run a sequence of models with 1-10 classes and print out the model with the lowest BIC
max_II <- -100000
min_bic <- 100000
for(i in 2:10){
lc <- poLCA(f, mydata, nclass=i, maxiter=3000,
tol=1e-5, na.rm=FALSE,
nrep=10, verbose=TRUE, calc.se=TRUE)
if(lc$bic < min_bic){
min_bic <- lc$bic
LCA_best_model<-lc
}
}
LCA_best_model
You´ll get the standard-output for the best model from the poLCA-package:
Conditional item response (column) probabilities,
by outcome variable, for each class (row)
$F29_a
Pr(1) Pr(2) Pr(3) Pr(4) Pr(5) Pr(6) Pr(7)
class 1: 0.0413 0.2978 0.1638 0.2487 0.1979 0.0428 0.0078
class 2: 0.0000 0.0429 0.0674 0.3916 0.4340 0.0522 0.0119
class 3: 0.0887 0.5429 0.2713 0.0666 0.0251 0.0055 0.0000
$F29_b
Pr(1) Pr(2) Pr(3) Pr(4) Pr(5) Pr(6) Pr(7)
class 1: 0.0587 0.2275 0.1410 0.3149 0.1660 0.0697 0.0222
class 2: 0.0000 0.0175 0.0400 0.4100 0.4249 0.0724 0.0351
class 3: 0.0735 0.4951 0.3038 0.0669 0.0265 0.0271 0.0070
$F29_c
Pr(1) Pr(2) Pr(3) Pr(4) Pr(5) Pr(6) Pr(7)
class 1: 0.0371 0.2082 0.1022 0.1824 0.3133 0.1365 0.0202
class 2: 0.0000 0.0086 0.0435 0.3021 0.4335 0.1701 0.0421
class 3: 0.0815 0.4690 0.2520 0.0903 0.0984 0.0088 0.0000
$F27_a
Pr(1) Pr(2) Pr(3) Pr(4) Pr(5) Pr(6) Pr(7)
class 1: 0.7068 0.2373 0.0248 0.0123 0.0000 0.0188 0.0000
class 2: 0.6914 0.2578 0.0128 0.0044 0.0207 0.0085 0.0044
class 3: 0.8139 0.1523 0.0110 0.0000 0.0119 0.0000 0.0108
$F27_b
Pr(1) Pr(2) Pr(3) Pr(4) Pr(5) Pr(6) Pr(7)
class 1: 0.6198 0.1080 0.0426 0.0488 0.1226 0.0582 0.0000
class 2: 0.6336 0.1062 0.0744 0.0313 0.1047 0.0370 0.0128
class 3: 0.7185 0.1248 0.0863 0.0158 0.0325 0.0166 0.0056
$F27_e
Pr(1) Pr(2) Pr(3) Pr(4) Pr(5) Pr(6) Pr(7)
class 1: 0.6595 0.1442 0.0166 0.0614 0.0926 0.0062 0.0195
class 2: 0.6939 0.1474 0.0105 0.0178 0.0725 0.0302 0.0276
class 3: 0.7869 0.1173 0.0375 0.0000 0.0395 0.0000 0.0188
$F09_a
Pr(1) Pr(2) Pr(3) Pr(4) Pr(5) Pr(6)
class 1: 0.8325 0.1515 0.0000 0.0000 0.0160 0.0000
class 2: 0.1660 0.3258 0.2448 0.1855 0.0338 0.0442
class 3: 0.1490 0.2667 0.3326 0.1793 0.0575 0.0150
$F09_b
Pr(1) Pr(2) Pr(3) Pr(4) Pr(5) Pr(6)
class 1: 0.8116 0.1594 0.0120 0.0069 0.0000 0.0101
class 2: 0.0213 0.3210 0.4000 0.2036 0.0265 0.0276
class 3: 0.0343 0.3688 0.3063 0.2482 0.0264 0.0161
$F09_c
Pr(1) Pr(2) Pr(3) Pr(4) Pr(5) Pr(6)
class 1: 0.9627 0.0306 0.0067 0.0000 0.0000 0.0000
class 2: 0.1037 0.4649 0.2713 0.0681 0.0183 0.0737
class 3: 0.1622 0.4199 0.2338 0.1261 0.0258 0.0322
Estimated class population shares
0.2792 0.4013 0.3195
Predicted class memberships (by modal posterior prob.)
0.2738 0.4055 0.3206
=========================================================
Fit for 3 latent classes:
=========================================================
number of observations: 577
number of estimated parameters: 155
residual degrees of freedom: 422
maximum log-likelihood: -6646.732
AIC(3): 13603.46
BIC(3): 14278.93
G^2(3): 6121.357 (Likelihood ratio/deviance statistic)
X^2(3): 8967872059 (Chi-square goodness of fit)
Generate table showing fitvalues of multiple models
Now i want to build a table for comparison of various model-fit values like this:
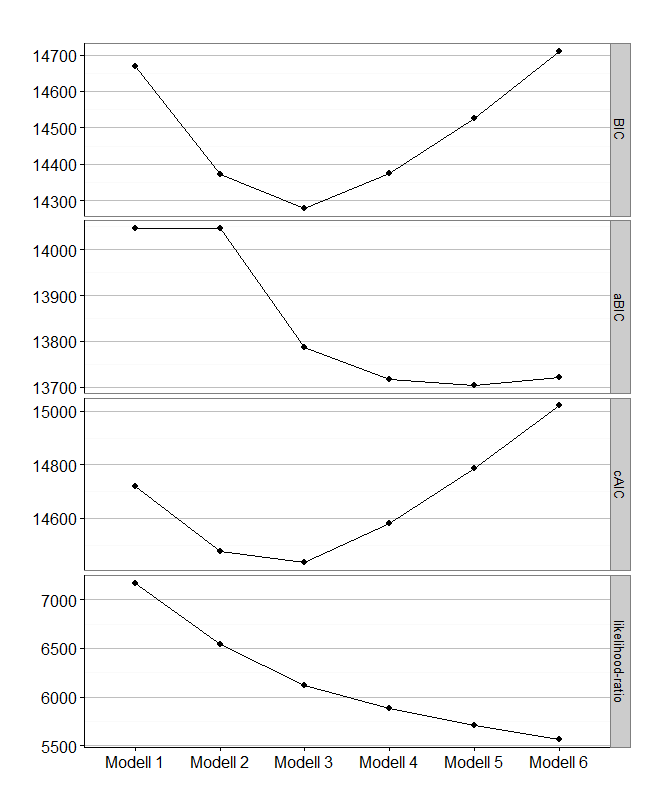
Modell log-likelihood resid. df BIC aBIC cAIC likelihood-ratio Entropy Modell 1 -7171.940 526 14668.13 14046.03 14719.13 7171.774 - Modell 2 -6859.076 474 14373.01 14046.03 14476.01 6546.045 0.86 Modell 3 -6646.732 422 14278.93 13786.87 14433.93 6121.357 0.879 Modell 4 -6528.791 370 14373.66 13716.51 14580.66 5885.477 0.866 Modell 5 -6439.588 318 14525.86 13703.64 14784.86 5707.070 0.757 Modell 6 -6366.002 266 14709.29 13721.99 15020.29 5559.898 0.865
This table was build by the following code:
#select data
mydata <- data %>% dplyr::select(F29_a,F29_b,F29_c,F27_a,F27_b,F27_e,F09_a, F09_b, F09_c)
# define function
f<-with(mydata, cbind(F29_a,F29_b,F29_c,F27_a,F27_b,F27_e,F09_a, F09_b, F09_c)~1)
## models with different number of groups without covariates:
set.seed(01012)
lc1<-poLCA(f, data=mydata, nclass=1, na.rm = FALSE, nrep=30, maxiter=3000) #Loglinear independence model.
lc2<-poLCA(f, data=mydata, nclass=2, na.rm = FALSE, nrep=30, maxiter=3000)
lc3<-poLCA(f, data=mydata, nclass=3, na.rm = FALSE, nrep=30, maxiter=3000)
lc4<-poLCA(f, data=mydata, nclass=4, na.rm = FALSE, nrep=30, maxiter=3000)
lc5<-poLCA(f, data=mydata, nclass=5, na.rm = FALSE, nrep=30, maxiter=3000)
lc6<-poLCA(f, data=mydata, nclass=6, na.rm = FALSE, nrep=30, maxiter=3000)
# generate dataframe with fit-values
results <- data.frame(Modell=c("Modell 1"),
log_likelihood=lc1$llik,
df = lc1$resid.df,
BIC=lc1$bic,
ABIC= (-2*lc1$llik) + ((log((lc1$N + 2)/24)) * lc1$npar),
CAIC = (-2*lc1$llik) + lc1$npar * (1 + log(lc1$N)),
likelihood_ratio=lc1$Gsq)
results$Modell<-as.integer(results$Modell)
results[1,1]<-c("Modell 1")
results[2,1]<-c("Modell 2")
results[3,1]<-c("Modell 3")
results[4,1]<-c("Modell 4")
results[5,1]<-c("Modell 5")
results[6,1]<-c("Modell 6")
results[2,2]<-lc2$llik
results[3,2]<-lc3$llik
results[4,2]<-lc4$llik
results[5,2]<-lc5$llik
results[6,2]<-lc6$llik
results[2,3]<-lc2$resid.df
results[3,3]<-lc3$resid.df
results[4,3]<-lc4$resid.df
results[5,3]<-lc5$resid.df
results[6,3]<-lc6$resid.df
results[2,4]<-lc2$bic
results[3,4]<-lc3$bic
results[4,4]<-lc4$bic
results[5,4]<-lc5$bic
results[6,4]<-lc6$bic
results[2,5]<-(-2*lc2$llik) + ((log((lc2$N + 2)/24)) * lc2$npar) #abic
results[3,5]<-(-2*lc3$llik) + ((log((lc3$N + 2)/24)) * lc3$npar)
results[4,5]<-(-2*lc4$llik) + ((log((lc4$N + 2)/24)) * lc4$npar)
results[5,5]<-(-2*lc5$llik) + ((log((lc5$N + 2)/24)) * lc5$npar)
results[6,5]<-(-2*lc6$llik) + ((log((lc6$N + 2)/24)) * lc6$npar)
results[2,6]<- (-2*lc2$llik) + lc2$npar * (1 + log(lc2$N)) #caic
results[3,6]<- (-2*lc3$llik) + lc3$npar * (1 + log(lc3$N))
results[4,6]<- (-2*lc4$llik) + lc4$npar * (1 + log(lc4$N))
results[5,6]<- (-2*lc5$llik) + lc5$npar * (1 + log(lc5$N))
results[6,6]<- (-2*lc6$llik) + lc6$npar * (1 + log(lc6$N))
results[2,7]<-lc2$Gsq
results[3,7]<-lc3$Gsq
results[4,7]<-lc4$Gsq
results[5,7]<-lc5$Gsq
results[6,7]<-lc6$Gsq
Now i calculate the Entropy (a pseudo-r-squared) for each solution. I took the idea from Daniel Oberski´s Presentation on LCA.
entropy<-function (p) sum(-p*log(p))
results$R2_entropy
results[1,8]<-c("-")
error_prior<-entropy(lc2$P) # class proportions model 2
error_post<-mean(apply(lc2$posterior,1, entropy),na.rm = TRUE)
results[2,8]<-round(((error_prior-error_post) / error_prior),3)
error_prior<-entropy(lc3$P) # class proportions model 3
error_post<-mean(apply(lc3$posterior,1, entropy),na.rm = TRUE)
results[3,8]<-round(((error_prior-error_post) / error_prior),3)
error_prior<-entropy(lc4$P) # class proportions model 4
error_post<-mean(apply(lc4$posterior,1, entropy),na.rm = TRUE)
results[4,8]<-round(((error_prior-error_post) / error_prior),3)
error_prior<-entropy(lc5$P) # class proportions model 5
error_post<-mean(apply(lc5$posterior,1, entropy),na.rm = TRUE)
results[5,8]<-round(((error_prior-error_post) / error_prior),3)
error_prior<-entropy(lc6$P) # class proportions model 6
error_post<-mean(apply(lc6$posterior,1, entropy),na.rm = TRUE)
results[6,8]<-round(((error_prior-error_post) / error_prior),3)
# combining results to a dataframe
colnames(results)<-c("Model","log-likelihood","resid. df","BIC","aBIC","cAIC","likelihood-ratio","Entropy")
lca_results<-results
# Generate a HTML-TABLE and show it in the RSTUDIO-Viewer (for copy & paste)
view_kable <- function(x, ...){
tab <- paste(capture.output(kable(x, ...)), collapse = '\n')
tf <- tempfile(fileext = ".html")
writeLines(tab, tf)
rstudio::viewer(tf)
}
view_kable(lca_results, format = 'html', table.attr = "class=nofluid")
# Another possibility which is prettier and easier to do:
install.packages("ztable")
ztable::ztable(lca_results)
Elbow-Plot
Sometimes, an Elbow-Plot (or Scree-Plot) can be used to see, which solution is parsimonius and has good fit-values. You can get it with this ggplot2-code i wrote:
# plot 1
# Order categories of results$model in order of appearance
install.packages("forcats")
library("forcats")
results$model < - as_factor(results$model)
#convert to long format
results2<-tidyr::gather(results,Kriterium,Guete,4:7)
results2
#plot
fit.plot<-ggplot(results2) +
geom_point(aes(x=Model,y=Guete),size=3) +
geom_line(aes(Model, Guete, group = 1)) +
theme_bw()+
labs(x = "", y="", title = "") +
facet_grid(Kriterium ~. ,scales = "free") +
theme_bw(base_size = 16, base_family = "") +
theme(panel.grid.major.x = element_blank() ,
panel.grid.major.y = element_line(colour="grey", size=0.5),
legend.title = element_text(size = 16, face = 'bold'),
axis.text = element_text(size = 16),
axis.title = element_text(size = 16),
legend.text= element_text(size=16),
axis.line = element_line(colour = "black")) # Achsen etwas dicker
# save 650 x 800
fit.plot
Inspect population shares of classes
If you are interested in the population-shares of the classes, you can get them like this:
round(colMeans(lc$posterior)*100,2) [1] 27.92 40.13 31.95
or you inspect the estimated class memberships:
table(lc$predclass) 1 2 3 158 234 185 round(prop.table(table(lc$predclass)),4)*100 1 2 3 27.38 40.55 32.06
Ordering of latent classes
Latent classes are unordered, so which latent class becomes number one, two, three... is arbitrary. The latent classes are supposed to be nominal, so there is no reason for one class to be the first. You can order the latent classes if you must. There is a function for manually reordering the latent classes: poLCA.reorder()
First, you run a LCA-model, extract the starting values and run the model again, but this time with a manually set order.
#extract starting values from our previous best model (with 3 classes) probs.start<-lc3$probs.start #re-run the model, this time with "graphs=TRUE" lc<-poLCA(f, mydata, nclass=3, probs.start=probs.start,graphs=TRUE, na.rm=TRUE, maxiter=3000) # If you don´t like the order, reorder them (here: Class 1 stays 1, Class 3 becomes 2, Class 2 becomes 1) new.probs.start<-poLCA.reorder(probs.start, c(1,3,2)) #run polca with adjusted ordering lc<-poLCA(f, mydata, nclass=3, probs.start=new.probs.start,graphs=TRUE, na.rm=TRUE) lc
Now you have reordered your classes. You could save these starting values, if you want to recreate the model anytime.
saveRDS(lc$probs.start,"/lca_starting_values.RData")
Plotting
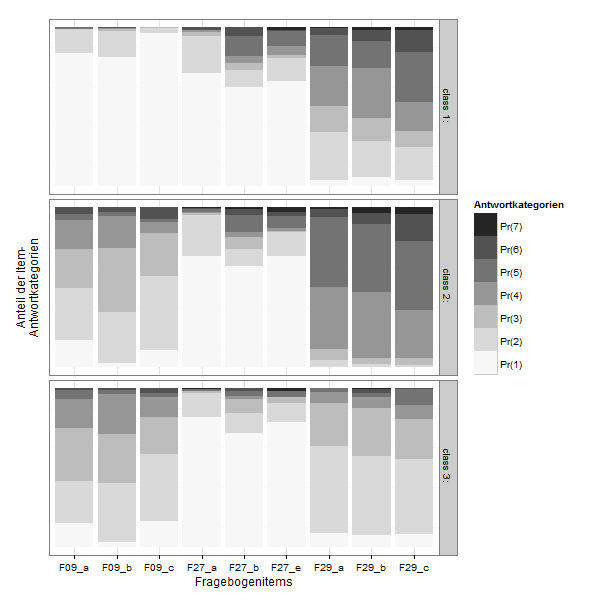
This is the poLCA-standard Plot for conditional probabilites, which you get if you add "graph=TRUE" to the poLCA-call.
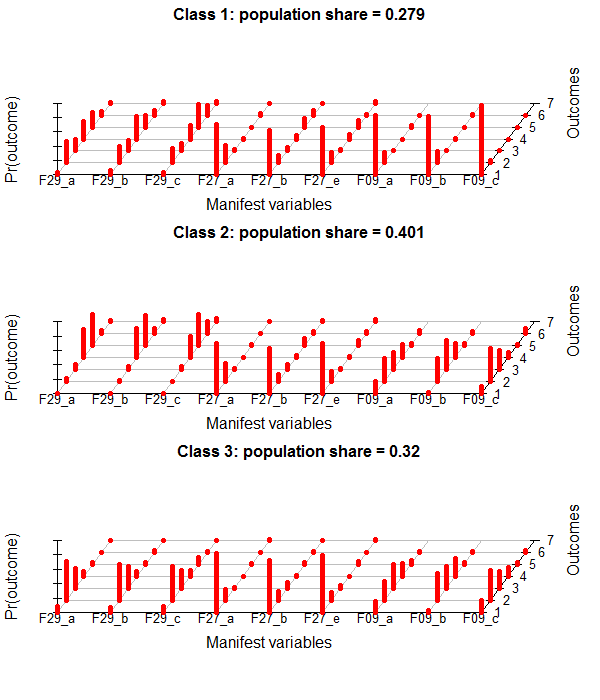
It´s in a 3D-style which is not really my taste. I found some code at dsparks on github or this Blog, that makes very appealing ggplot2-plots and did some little adjustments.
lcmodel <- reshape2::melt(lc$probs, level=2)
zp1 <- ggplot(lcmodel,aes(x = L1, y = value, fill = Var2))
zp1 <- zp1 + geom_bar(stat = "identity", position = "stack")
zp1 <- zp1 + facet_grid(Var1 ~ .)
zp1 <- zp1 + scale_fill_brewer(type="seq", palette="Greys") +theme_bw()
zp1 <- zp1 + labs(x = "Fragebogenitems",y="Anteil der Item-\nAntwortkategorien", fill ="Antwortkategorien")
zp1 <- zp1 + theme( axis.text.y=element_blank(),
axis.ticks.y=element_blank(),
panel.grid.major.y=element_blank())
zp1 <- zp1 + guides(fill = guide_legend(reverse=TRUE))
print(zp1)
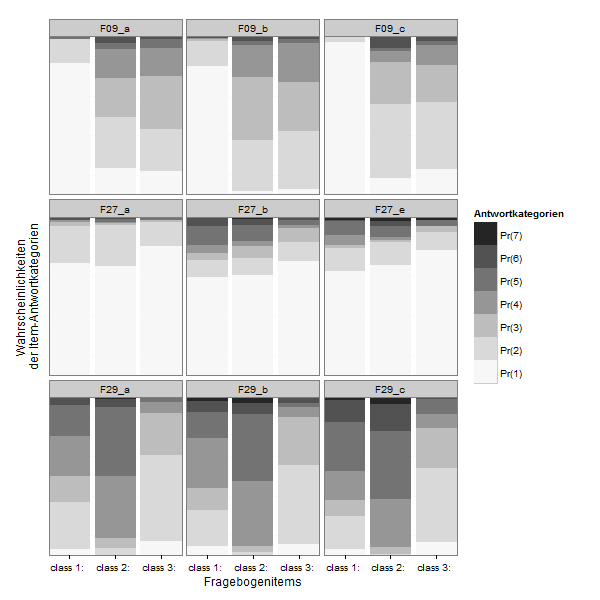
If you want to compare the items directly:
zp2 <- ggplot(lcmodel,aes(x = Var1, y = value, fill = Var2))
zp2 <- zp2 + geom_bar(stat = "identity", position = "stack")
zp2 <- zp2 + facet_wrap(~ L1)
zp2 <- zp2 + scale_x_discrete("Fragebogenitems", expand = c(0, 0))
zp2 <- zp2 + scale_y_continuous("Wahrscheinlichkeiten \nder Item-Antwortkategorien", expand = c(0, 0))
zp2 <- zp2 + scale_fill_brewer(type="seq", palette="Greys") +
theme_bw()
zp2 <- zp2 + labs(fill ="Antwortkategorien")
zp2 <- zp2 + theme( axis.text.y=element_blank(),
axis.ticks.y=element_blank(),
panel.grid.major.y=element_blank()#,
#legend.justification=c(1,0),
#legend.position=c(1,0)
)
zp2 <- zp2 + guides(fill = guide_legend(reverse=TRUE))
print(zp2)